“三维世界”的概念,我们早已耳熟能详,但第四维的概念常常蒙着一层惹人疑惑的神秘色彩。作为被长度、高度和宽度所限的生物,我们哪儿来的胆量高谈阔论四维空间?用尽我们三维头脑的所有智慧,是否有可能想象出四维超空间的模样?
四维的立方体或者球体看起来会是什么样子?
如果要你想象一头尾巴长满鳞片、鼻孔喷出火焰的巨龙,或者一架内设游泳池、机翼上有网球场的奢华飞机,你会在脑海中绘出一幅画面,试图描摹这件物体突然出现在你眼前的时候会是什么模样。
而这幅画的背景自然是正常的三维空间,你熟悉的所有物体,包括你自己在内,都存在于这样的空间里。如果这就是“想象”的确切含义,那么我们似乎不太可能想象出以正常三维空间为背景的四维物体,正如三维物体不可能被挤进平面一样。
但是,等等,从某种意义上说,我们的确能将三维物体压进平面,只要画一幅画就行。
不过在这种情况下,我们借助的当然不是液压机床或者其他什么物理力量,而是一种名为几何“投影”的绘画技巧。要将某件物体(比如说一匹马)压进平面,看看下图,你立即就会明白这两种方式有何区别。
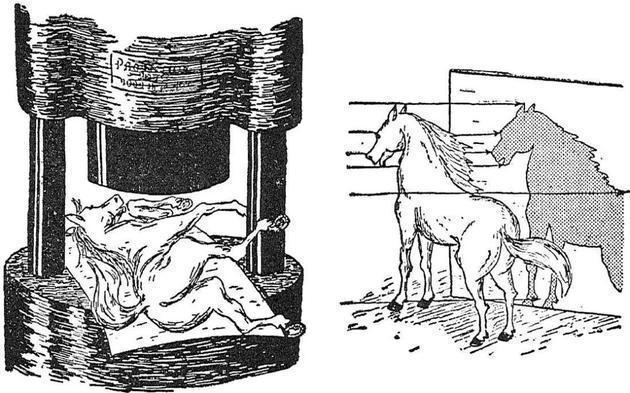
将三维物体“压在”二维面上的两种方法,左边的方法是错的,右边的法子才对
以此类推,现在我们可以说,如果非要将四维物体“挤入”三维空间,那它难免会有些零件左右支棱,但我们的确可以讨论各种四维图形在我们这个三维空间中的投影。不过你必须记住,既然三维物体在二维面上的投影只有两个维度,那么四维超物体在普通三维空间内的投影也必然是三维的。
为了更清楚地理解这一点,首先我们不妨试想一下,生活在二维面上的影子生物该如何理解三维立方体的概念;我们能够轻而易举地想象这一幕,是因为我们生活在“更高级”的三维空间里,所以我们才能从上方,也就是从第三个方向,观察这个二维世界。
要将一个立方体“压进”二维面,唯一的办法就是按照下图所示的方法将它“投射”到这个面上。如果我们的二维朋友看到这个投影,以及旋转立方体得到的其他方向的投影,那么他们至少会对这个名为“三维立方体”的神秘物体形成一些粗浅的理解。
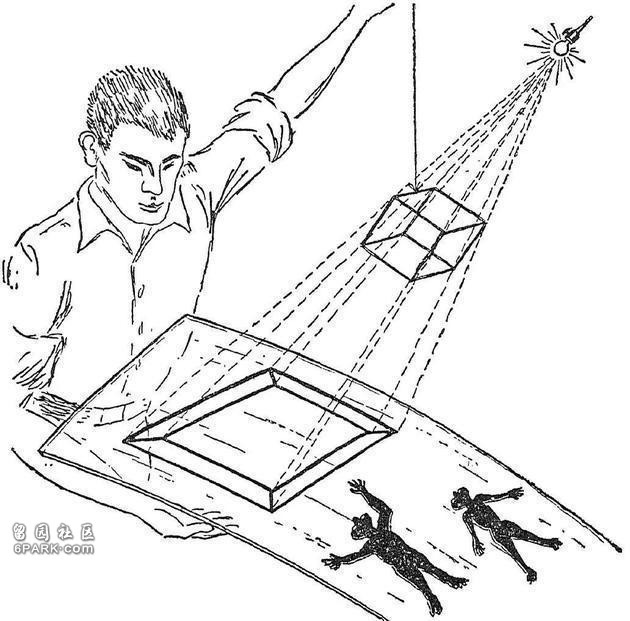
二维生物惊讶地望着三维立方体投射在他们生活的二维面上的影子
他们当然无法“跳出”自己所在的二维空间,像我们一样亲眼观察这个立方体的模样,但通过二维投影,他们至少会发现,这个立方体拥有8个顶点和12条边。现在看看下面那张图,你会发现自己的处境和那些在二维面上研究三维立方体的可怜的影子生物完全一样。
画面上这惊奇的一家子正在研究的那个复杂的奇怪结构实际上是四维超立方体在普通三维空间内的投影。(更确切地说,你在下面这张图中看到的是四维超立方体在三维空间内的投影在二维纸面上留下的投影。)
仔细研究这个图形,你很容易发现超立方体的一些特性,和上图中那些困惑的影子生物观察到的差不多:三维立方体在平面上的投影表现为两个嵌套正方形,它们的顶点两两相连;而超立方体在三维空间内的投影由两个嵌套立方体组成,顶点同样两两相连。
数一数你就知道,这个超立方体一共有16个顶点,32条边和24个面。看起来真够怪的,对吧?
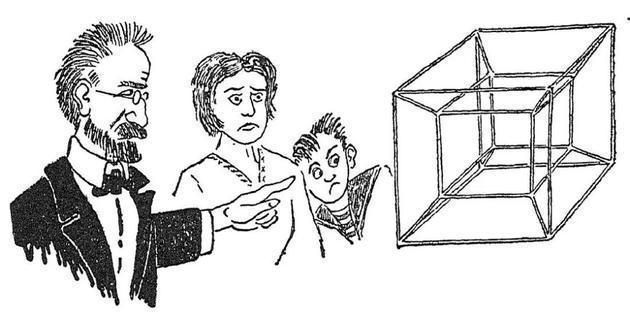
来自第四维的客人!四维超立方体的直接投影
现在,我们再来看看四维球体是什么样的。要完成这个目标,我们最好换个更熟悉的例子,就是普通球体在二维面上的投影。假设有一个透明的地球仪,上面标出了所有的大洲和大洋,现在我们将它投影到一面白墙上(如下图)。
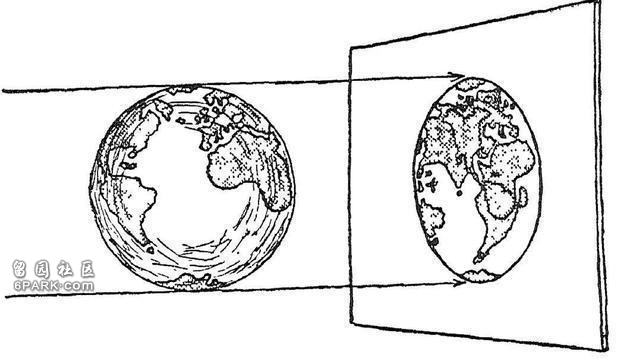
地球的平面投影
当然,在这幅投影图中,前后两个半球必然重叠,要是只看投影,你没准会觉得美国纽约和中国北京隔得很近。但这是一个错误的印象。
事实上,投影上的每一个点都代表着实际球体上两个相对的点,如果有一架航班从纽约飞往中国,那么你将看到,飞机先是一路朝着平面投影的边缘移动,然后再原路返回。两个不同航班在投影图上的航迹可能重叠,但只要这两架飞机“实际”上位于两个不同的半球,那它们绝不会迎面撞上。
以上就是普通球体二维投影的特性。再发挥一点想象力,我们应该不难揣想四维超球体在三维空间内的投影会是什么样。
三维球体在二维面上的投影是两个点对点重叠的圆盘,它们只通过共同的边缘相连;那么超球体的三维投影必然是两个重叠的球体,只通过共同的表面相连。这个奇特的结构我们在上一章中已经讨论过了,当时我们举这个例子是为了说明类似封闭球面的封闭三维空间。
所以现在,我们只需要补充一句:四维球体的三维投影就是上一章中那个连体婴儿般的“双重苹果”,它由两个果皮完全重叠的苹果组成。(如下图)
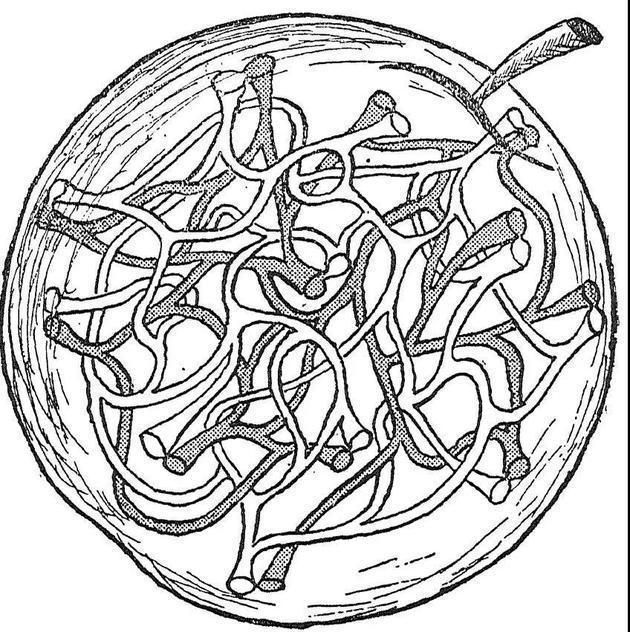
以此类推,我们还可以回答关于四维物体特性的很多问题。只是无论怎么尝试,我们可能都无法“想象”,我们这个物理空间中还有第四个独立的维度。
三维空间中的任意位置都能用前后、左右、上下三个维度来表达。如果我们来到一座陌生的城市,询问酒店前台某家著名公司的位置,那么店员也许会说:“往南走五个街区,然后右转经过两个街区,直接上七楼。”
这三个数字通常被称为坐标,事实上,要前往一个确定的目的地,无论起点如何变化,只要有一套能够正确描述新起点与目的地之间方位关系的坐标系,我们总能找到正确的方向。
而第四个维度难以想象的原因在于,它不受前后、左右、上下这三个维度的控制,在人们的头脑里,它是“空间”(三维世界)之外的奇怪存在。
但只要再想想,你会发现第四个维度其实并不神秘。有一个东西,它不受前后、左右、上午的控制,而且,我们不会把它和“空间”联系在一块儿。这个东西我们大部分人每天都会用到,它可以被视为、而且实际上就是物理世界中的第四个维度,这个词就是“时间”。
在我们描述周围发生的事件时,时间常常是一个和空间并列的度量。当我们谈到宇宙中发生了什么,无论是你在街上意外邂逅了一位老朋友,还是一颗遥远的恒星发生了爆炸,一般情况下,我们不光会提到事件发生的位置,还会陈述它发生的时间。通过这种方式,我们为三维空间中的事件引入了第四个维度:日期。
进一步思考这个问题,你也很容易发现,每个物理物体都有四个维度,其中三个是空间维度,还有一个是时间维度。你住的房子在长度、宽度、高度和时间这四个维度上延展,它在时间维度上的跨度始于建成之日,终于毁灭那一天——无论是烧毁、拆毁还是因年久失修而倒塌。
确切地说,时间这个维度和空间的三个维度不太一样。时间的跨度(间隔)由钟表来度量,秒针嘀嗒嘀嗒,整点叮咚报时;而测量空间距离的工具是尺子。你可以用同一把尺子测量长度、宽度和高度,但却不能把它变成钟来测量时间。
除此以外,你可以在空间中向前、向右或者向上移动,然后再返回原地,但时间一路向前,从不回头,你只能被动地从过去来到现在,再去往未来。这是第四个维度和空间的三个维度最不同的地方:它变了就是变了,无法复原。
尽管时间的维度和空间的三维有这么多的不同之处,但我们依然可以将时间当成第四个维度,用它来描述这个世界上的物理事件,只是不要忘了,时间和空间的确不太一样。
选定了时间作为第四个维度以后,我们会发现,想象本章开头提及的四维图形变得简单多了。比如说,你还记得那个四维立方体的奇怪投影吧?它有16个顶点、32条边和24个面!面对这样的几何怪胎,难怪看到四维立方体的人都一脸惊讶。
但是,现在我们换个角度来看,四维立方体实际上是一个存在于特定时间段内的普通立方体。假设你在5月7日用12根线搭了一个立方体,一个月后再把它拆了,那么现在,立方体的每个顶点都可被视作时间维度上跨度为一个月的一条线。你可以在立方体的每个顶点上贴一本小小的日历,然后每天翻一页,借此表示时间的流逝。
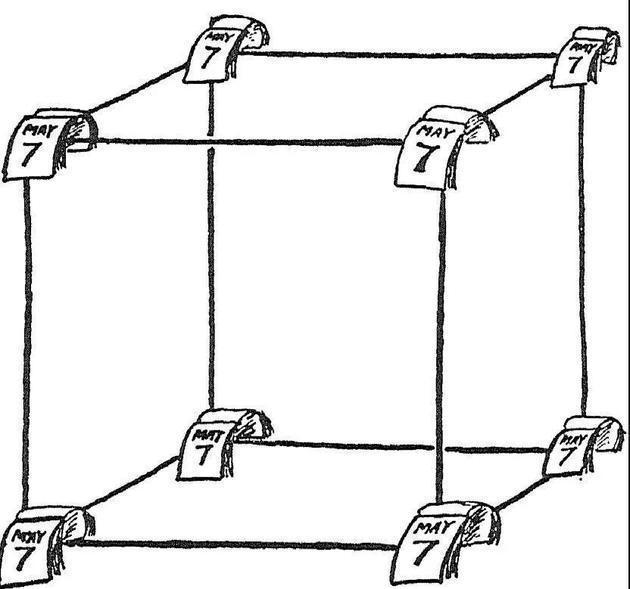
现在我们可以轻松数出这个四维图形有几条边了。事实上,这个立方体从诞生之初起就拥有空间中的12条边,然后在时间维度上它还拥有8个顶点拉出的8条边,最后,在被拆毁的那一天,它在空间中还有12条边。(如果你还是无法理解,不妨想像一个拥有4个顶点和4条边的正方形,如果我们在垂直于这个正方形的方向(第三个维度)上将它移动一段等于其边长的距离,它就会变成一个立方体。)一共32条边。
以此类推,我们也可以数出16个顶点:5月7日有8个空间顶点,6月7日也有8个空间顶点,总计16个顶点。至于这个四维立方体的面应该怎么数,这个问题就留给各位读者自己练习吧。不过请记住,四维立方体的面有一部分是普通三维空间中的面,还有一部分则是“半空间半时间”的,它们的边就是从5月7日延展到6月7日的那几条时间维度上的线。
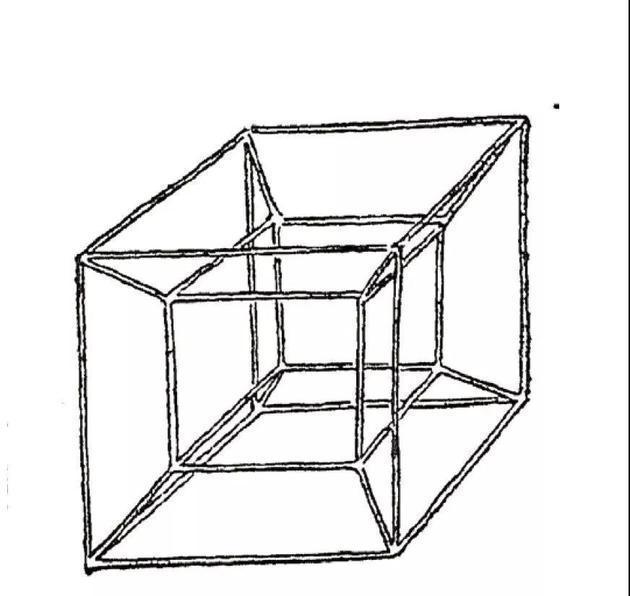
我们在此介绍的四维立方体的所有特性当然同样适用于其他任何几何图形或物体,无论是死的还是活的。
说到这里,我们可以想一想,怎样去理解自己在时间这个维度中的存在呢?
确切地说,你可以把自己想象成一个四维物体,类似在时间的长河里延展的一根长橡胶棒,它始于你的诞生之日,终于生命结束的时候。可惜的是,我们在纸上画不出这样的四维图形,所以在下图中,我们试着用二维的影子人代替三维的你,再将垂直于二维平面的时间作为第三个维度,力求帮助你理解这个概念。
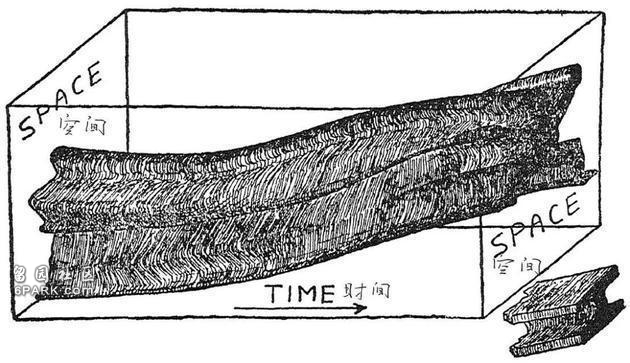
图中画出的只是这位影子人生命中的一小段时间,要想画出他的一生,那得换一根长得多的橡胶棒。起初这根棒子很细,因为影子人还小,漫长的几十年里,棒子不断扭动,直到影子人死亡那天才会凝固下来(因为死人不会动),然后开始崩解。
更准确地说,这根四维橡胶棒实际上分为无数根彼此独立的纤维,每根纤维内部又有许多互不相干的原子。在你的一生中,大部分纤维会始终聚合在一起形成一束,只有一小部分会中途散逸,比如说在你剪头发或者剪指甲的时候。既然原子不会毁灭,那么我们可以认为,人死后尸体腐烂的过程其实就是所有独立纤维(可能除了构成骨骼的那些纤维以外)分道扬镳,四下弥散。


