为什么全世界人民都喜爱π?只是一个数字而已,它有什么能耐?还真不小!今天让我们跟随大数据君一起,重新认识一下,这个你最熟悉的“陌生人”。

01 π里藏着所有人的银行卡密码?
π是无限不循环小数,也就是说π小数点后面的数字是无穷无尽的,并且是毫无规律的。
但盯着这些数字看,你可能会根据自己的主观需求给这些数字赋予一些特殊含义。比如,数据叔有个小学同学,是某年9月26日出生的。学习π的时候,这位同学就很自豪地说π里有他的生日(3.1415926),让我们这些小伙伴羡慕不已,感慨自己生错了时代日期。
那么如果是更多位的“特殊含义”的数字呢?比如,每个人的银行卡密码都是6位,那么问题来了,π小数点后面,是否会有连续的6位数字,恰好是你的银行卡密码?
1. 银行卡密码
数据叔找到一个查询特定数字组合是否会出现在π小数点后前20亿位的网站,玩了一个下午,你也可以去玩一下,网址是:
https://www.subidiom.com/pi/pi.asp
接下来说说数据叔都玩了什么。首先,我试了一下被称为“最烂密码”的123456:
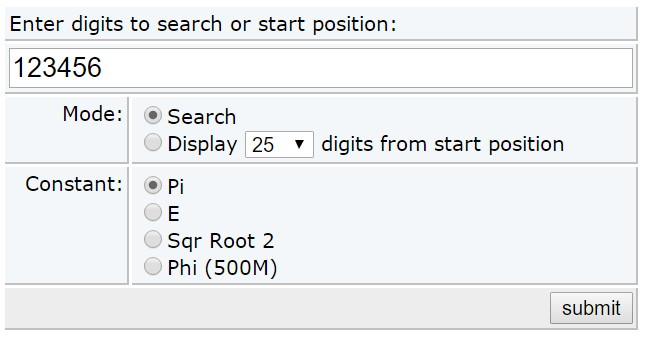
结果,123456这个组合在π中是存在的,从π小数点后的第2,458,885位开始出现。
然后,数据叔试了一下自己的银行卡密码,结果也没逃脱π的魔掌。截图就不上了。
实际上,早有大神跑过一个程序,证明了所有的6位数字组合——从000000到999999,都会出现在π的小数点后面,最后出现的组合是569540,位于小数点后14,118,307位[1]。所以,上面那个网站提供的前2,000,000,000位,有点资源过剩。于是,数据叔就想延长数字组合的长度,挑战一下这个网站的极限。
2. 生日
每个人的生日都可以用一个8位数字组合表示。π是一个超越数,数据叔就想到了最近忙着带盐编程大赛的杨超越。某百科资料显示,杨超越的生日是19980731,到网站查询一下,结果杨超越没能超越π的前20亿位:

再试试程序猿的老婆新垣结衣的生日19880611,结果也一样:

与银行卡密码的情况相同,也有大神在π的10亿位之内跑出了所有人的生日。但如果我们再增加数字组合的长度呢?
3. 手机号
中国大陆的手机号码都是11位,郝云有一首歌叫《结了》,歌词里唱出一个手机号:13910733521(这是真实存在的手机号,归属北京移动,但我劝你没事不要骚扰人家),我们就先试试这个手机号:

结果是,π小数点后的前20亿位中不包含这个数字组合,数据叔第一次“赢了”π。
数据叔又试了自己的号码,也是不存在;又打开通讯录,试了几个朋友的号码,还是不存在。你也可以拿自己和朋友的手机号试一试。看来,数字组合延长到11位,就没那么容易出现了,但我们也只是查询了π小数点后的前20亿位而已,π小数点后面还有无穷无尽的位。
02 圆周率钢琴曲:请开始你的表演
有人把数字写进歌词,还有人直接把数字改编成钢琴谱。YouTube用户aSongScout上传了这首“圆周率钢琴曲”:
03 什么是无理数?是没有道理的数吗?
无理数,即无限不循环小数,不能写作两整数之比。若将它写成小数形式,小数点之后的数字有无限多个,并且不会循环。
π不但是无理数,而且是超越数。超越数是代数运算不能操作的数。举例来说,根号2是无理数,但根号2可以用一个代数等式来表达:y=x2-2。而π却不能通过这样的等式表达。超越数无法通过加、减、乘、除、指数和求根运算的代数等式来描述。
很久很久以前,追求完美的数学家们非常不待见无理数,甚至还酿成过惨案。《数学极客:探索数字、逻辑、计算之美》一书中写道:
很多人也说,之所以称之为无理数是因为它们根本就没有道理,它们仅仅是存在即合理的体现罢了。
它们其实是有道理的,但是它们让很多数学家觉得不舒服。
《数学极客》中还提到了一个无理数引发的惨案:古希腊时期,毕达哥拉斯(Pythagoras)的学生希帕索斯(Hippasus)证明了根号2不能表示成任何两个整数比值。但毕达哥拉斯坚信数字是完美的,不能接受无理数的存在。
当他分析了希帕索斯的证明后,没有能够从中找到错误的地方,因此他变得恼羞成怒,一怒之下,把可怜的希帕索斯给淹死了。
04 圆周率节,我们是认真的
随着人类文明的进步,无理数也终于“翻了身”,不但被接受,而且像π、e、φ等特殊无理数都聚集了一群极客粉丝团,建立了文化生态。
1988年3月14日,物理学家Larry Shaw在旧金山探索中心组织了一场圆周率节(Pi Day)庆祝活动。这是我们迄今可以考证的人类历史上最早的圆周率节大规模庆典。参与者围绕着一个圆形空间散步,然后,他们吃了水果派。(没有传统美食的节日都是耍流氓。)

一个圆周率节促销售价3.14刀的派,拍摄者:TJRC,来源:Wikimedia Commons
此后,旧金山探索中心每年都会继续举办圆周率节庆祝活动。2009年,圆周率节(Pi Day)及其名称甚至得到了美国众议院的官方确认[2]。
类似的庆祝活动逐渐在世界各地兴起,并在互联网时代,从线下发展到了线上。圆周率节的网站(piday.org)也被建立起来,除了π和圆周率节的一些科普内容外,这个网站还在卖产品——一款名叫覆盆子派(Raspberry Pi)的电路板。
2010年3月14日,Google上线了圆周率节Google Doodle,设计中包含了π值范围,圆的周长与面积公式,球体、圆柱体体积公式等元素。
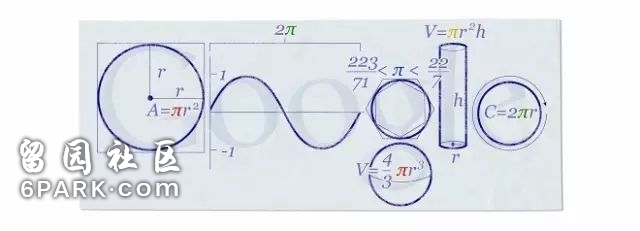
2010年3月14日的Google Doodle
2018年3月14日,为纪念Larry Shaw“发明”圆周率节30周年,Google上线了另一款圆周率节Google Doodle,并拍摄了大厨Dominique Ansel制作这个派的视频。于是,跟2010年的Google Doodle相比,2018款看起来很……好吃!

2018年圆周率节的Google Doodle,派的“周长”与“直径”用不同食材制作,构成等式C/d=π
另外,3月14日对于极客们来说也真是非常特别一天:1879年3月14日,爱因斯坦出生;2018年3月14日,霍金逝世。
说了这么多,最后提醒你,过节了,别忘了吃派!
相关报道:π日说π:“圆”可不可以不是圆的?
3月14日,也是的所谓的“π日” (Pi day)。 2011年,国际数学协会正式宣布,将每年的3月14日设为国际数学节。π不仅仅在几何学、数论和统计学等方面有着广泛的应用,同时也在宇宙学、热力学、力学和电磁学等领域中大放异彩。所以今天小编就带大家(回想起被数学支配的恐惧)一起感受圆和圆周率的魅力吧。
某不存在的网站上庆祝π日的Doodle,2010年3月14日。
01
“π”是什么
π的中文名字是圆周率,是一个数学常数,定义为圆的周长和其直径的比值,约等于3.1415926535897......。大约在18世纪中期之后,人们开始用希腊字母π来指代它,所以有时也会拼写为“pi”。
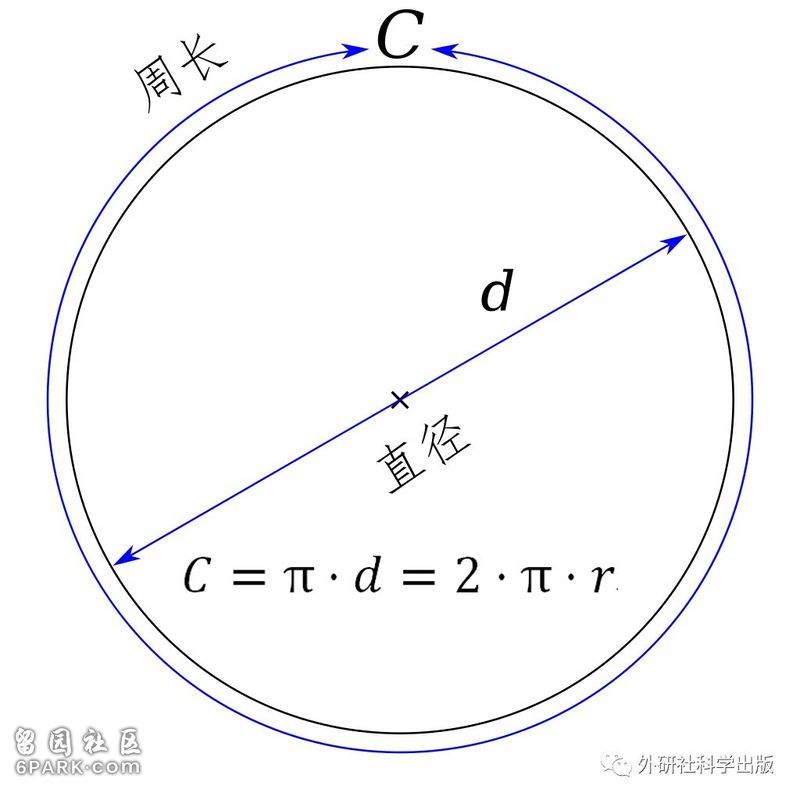
圆周率π的朴素定义(不朴素的定义详见下文)
关于π的值3.1415926535897......,它是一个无理数(也就是说π是无限不循环小数),同时也是一个超越数(所谓“超越数”,是指不满足任何整系数多项式方程的实数的数)。


“超越数”这个名字出自欧拉1748年的评论:“它们超越代数方法所及的范围之外。”但直到1844年,超越数的存在性才被法国数学家刘维尔证明。
02
“圆”可不可以不圆?
不知道有没有小伙伴会与小编有类似的问题,圆形可不可以不是圆的呢(这是何等握草的脑回路)?如果圆形不是圆的,那么世界又会发生什么变化呢?
要弄清这个问题,首先让我们从定义出发,想一想“圆”到底是个什么东东?
喵星人亲自示范如何让自己变圆
生活中圆形的东西比比皆是,不过为了让文章的叙述更为科学(B格更高),我们借用小学生数学课上对于圆的定义:“在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周所形成的封闭曲线叫做圆。”

当然各位看官自然不是小学生,所以我们改用更为高级一点(其实并没有)的语言描述一下这个问题。根据欧几里德的《几何原本》定义,圆是在同一平面内到定点的距离等于定长的点的集合。
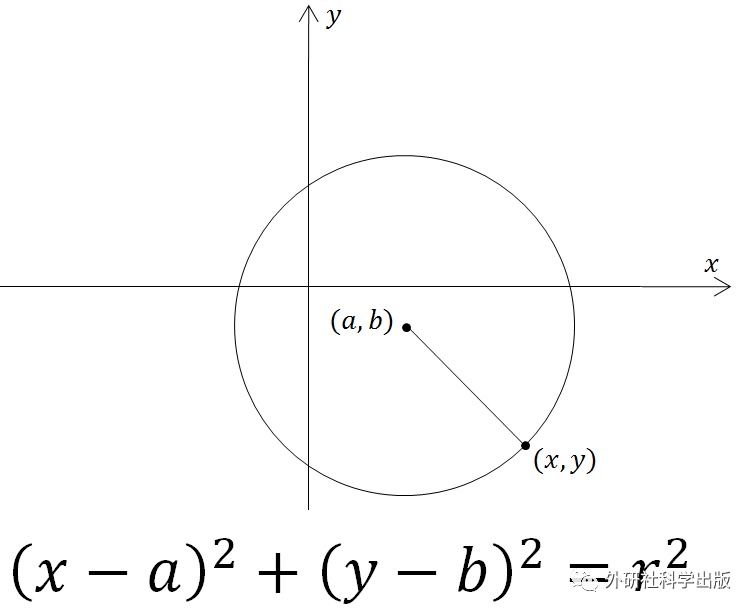
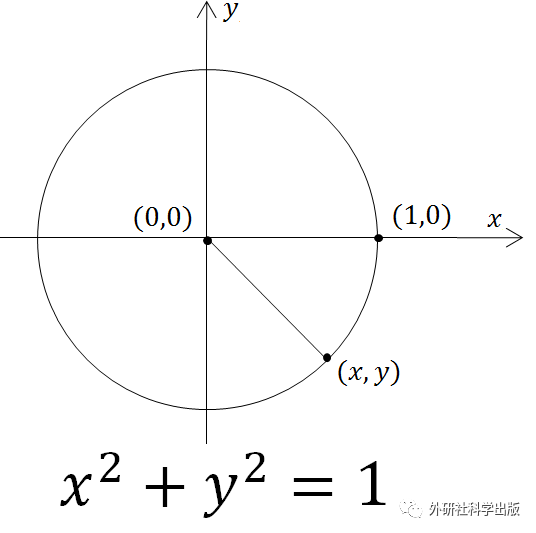
圆的标准方程。两个方程所代表圆的区别在于圆心的位置和半径的大小。
由此看来,一切问题的出发点都可以归结到两点之间的距离。那么问题来了,距离的本质是什么?


这里我们引入范数(norm,这可是连牛津高阶也查不到的翻译?)的概念。简单而言,范数可以认为是“距离”或者“长度”概念的推广。而在众多范数中,p-范数与我们的生活最为接近。

范数的严格定义(实际上似乎也不够严格,因为此处应该首先介绍半范数,不过毕竟篇幅(读者老爷们的耐心)有限)。有兴趣的同学可以参考任意一本书名中带有“泛函分析”字样的教科书。
p-范数,又称为lp-范数,“l”这里指的是法国数学家亨利·勒贝格(Henri Léon Lebesgue)。这里留一道家庭作业,为什么p-范数定义中要求p大于等于1?
前面讲到的p=2的情形(欧几里德范数),实际上就对应了我们日常生活中所说的“距离”,即在笛卡尔坐标系下两点间的距离公式。当然平面几何中不需要n维向量,只需要二维向量(x,y)就足够了。
二维平面上的两点间距离公式。细心的小伙伴可能已经发现距离公式和前面提到的圆的方程非常相似。事实上,这里给出的两个公式恰好对应前面图中的两个圆。
现在让我们再次回到单位圆的问题,考虑一下在不同范数下单位圆的形状有何不同。
当p取不同数值时,“单位圆”的形状。考虑到所有的圆形都可以视为单位圆改变圆心位置和/或改变半径后的产物,所以为了方便起见,这里就给出单位圆的形状。
显然随着p的增大,“单位圆”也就变得越来越胖,而且经历了“由方变圆又变方”的奇妙旅程?
03
π能不能不等于3.1415926......
既然“单位圆”都可以不是圆的,那么我们不禁要问,π能不能不等于3.1415926......呢?
这个问题其实就已经有点接近数学家的恶趣味了,不过还是在文章的最后(不顾读者的骂声)简要地讲一讲吧。
我们首先考虑极限情况,也就是让p趋近于无限大,那么我们就得到了下面的图形。(没错,就是刚才的图又放了一遍)考虑到圆的面积S等于π乘以半径的平方。由于下面这个图形也属于“单位圆”,所以它的半径就是1,于是我们就得到了上面图形的面积S数值上等于π!由于S这里等于4,所以这种情况下π=4?!(这都是什么鬼)
上面所讲的虽然有些无厘头(事实上是错误的示范?),但是最终π=4的结论是没有问题的。(思考题:正确的思路应该是怎样的呢?)考虑到p=1的时候得到的图形本质是跟p趋于无穷时没有什么不同,所以p=1同样应该对应π=4。这里推荐C. L. Adler 与 James Tanton发表在《The College Mathematics Journal》上的文章(是的,你没有看错,这些东西都是College Mathematics?):
Adler, C. L. , and J. Tanton . "π is the Minimum Value for Pi." The College Mathematics Journal 31.2(2000): 102-106.
这里我们用Mathematica软件重现了一下文章的结果。
上面图像是范数p的取值与π关系。横坐标为范数p的取值,纵坐标是在不同范数的情况下“圆周率”的取值。图像是依据下面展示的公式绘制的。最后给出一组具体的数值供同学们参考。
由此可见,虽然π本身似乎可以乱动,但是3.1415926......确乎有着某种特殊的意义,至少它是所有可能的π中最小的一个。



