如果数学是宇宙的语言,蜜蜂可能刚刚说出它们的第一个单词。一项于 2 月 7 日发表在 Science Advances 的新研究表明,看起来并不起眼的蜜蜂竟然能够使用符号演算包括加减法在内的基础算术。
尽管蜜蜂的大脑只有不到 100 万个神经元,非常小。但近期的一些研究发现,它们能够处理一些较为复杂的问题——比如理解“0”的概念,同时,它们能学会基础算术。
加减法运算

早在孩童时期,我们便知道一个加号(+)表示我们需要将两个或更多的数量相加,而减号(-)则意味着我们要用一个数量中减掉另一个数量。
当我们在解决这些问题时,我们需要将长期记忆与短期记忆共同运用。在进行运算时,我们利用短期记忆去处理运算中的具体数值,利用长期记忆储存加法或减法的运算规则。
尽管学会加减法等运算并不简单,但这一能力对人类社会而言非常重要。古埃及和古巴比伦的古迹中,在公元前 2000 年左右便有人类使用算术的证据——如对家畜计数,并在出售后减去相应的数字。
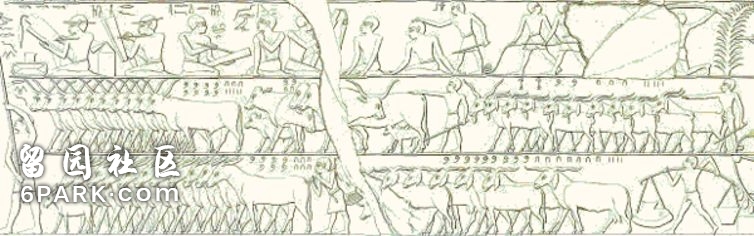
图|这幅画(来自埃及古物学家Lepsius 的复制版)描绘了对家畜计数的场景。中间一行可以看到左边有 835 只有角家畜,紧随其后的是约 220 只其他动物,右边有 2235 只山羊。最下一行左边有 760 只驴,右边有 974 只山羊。(图片来源:Wikimedia commons)
但发育出算术思维是否必须要有一个灵长类大脑,抑或是其他动物面对类似问题时也能进行运算?研究人员使用蜜蜂来研究这个问题。
如何训练蜜蜂

每只蜜蜂单独在 Y 型迷宫装置中接受训练。
当蜜蜂飞到 Y 型迷宫的入口时,会看到一排由 1 到 5 个形状组成的图案。这些形状(如:正方形)由 1 到 2 种颜色组成。蓝色意味着蜜蜂需要进行加法运算(+1),黄色意味着蜜蜂要做减法(-1)。
在加减 1 的任务中,迷宫一边是不正确的答案,另一边是正确的答案。在整个实验过程中,正确答案的位置会随机改变,这样蜜蜂就不会学习只访问 Y 型迷宫的一边。
在浏览过初始数字后,每只蜜蜂会从一个孔里飞到选择室中,在那里它可以选择飞到 y 迷宫的左边或右边,这取决于它所接受的训练。
由于蜜蜂是中心位置觅食者(central place foragers),这意味着蜜蜂在觅食后会回到特定中心位置,而后会再次返回食物充足的地点重复觅食。
研究人员的实验装置给蜜蜂提供了高浓度糖水,所以工蜂(均为雌性)会不停返回该装置为蜂巢采集食物。当蜜蜂选择了正确数字,它将得到糖水奖励;如果它选错了,将会得到苦味的奎宁水。
利用这种方法,研究人员在 4-7 小时不等的时间内教会了蜜蜂加减法运算。每次蜜蜂采集食物后将返回蜂巢,随后它们还会返回实验装置并继续学习。
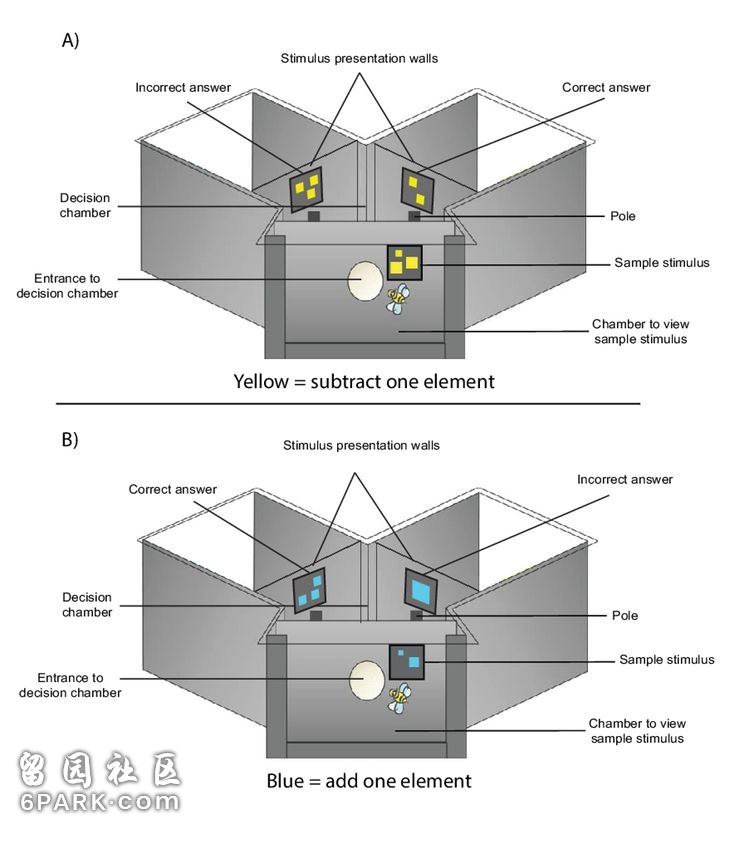
图|用来训练蜜蜂的 Y 型迷宫装置。(图片来源:Scarlett Howard)
在实验的一开始,蜜蜂只会的随机做出选择,直到它们发现了解决问题的方法。最终,经过100 多次训练,蜜蜂学会了蓝色意味着+1、黄色意味着-1。然后蜜蜂可以将这些规则应用到新的数字上。
在对一个新的数字进行测试时,蜜蜂计算加减 1 时的正确率在 64-72% 范围内,显著优于蜜蜂随机做出选择的正确率(50% 正确/50% 错误)。
因此,研究人员认为 Y 型迷宫的“蜜蜂学校”能够教会蜜蜂如何使用运算符号做加减。
对人工智能及神经生物学的启示

对于蜜蜂而言,加减法等数学运算是个很复杂的问题,因为运算过程需要两级处理。第一级要求蜜蜂理解数值属性,第二级则要求蜜蜂在大脑的工作记忆中操纵数值。
除此之外,蜜蜂还需要在工作记忆中执行算术运算——数字“1”或加或减都不能展现在眼前。或者说,加减“1”的思维过程对于蜜蜂来说,是必须通过训练才能理解掌握的抽象概念。
在 AI 领域火热的今天,人们对计算机如何自我学习新问题很感兴趣。
蜜蜂作为动物模型,在神经科学领域具有很高价值。此次研究表明蜜蜂能够将简单的算术和符号学习结合起来,在这表示微型大脑也可以学会使用运算符号进行加减法。或许我们可以设计出使长期法则与工作记忆相结合的新方法、以此来提升 AI 在自我学习方面的表现。
同时,研究结果还表明,将数学符号理解为一种带有运算符的语言,是许多大脑都可能做到的,也有助于解释许多人类文明如何独立地发展出了计算能力,启发了许多有待拓展的研究领域。


