惩戒混乱,追寻规律,这是本届物理学奖得主的使命

3位获奖者因对复杂系统的研究成果，共同获得了今年的诺贝尔物理学奖。真锅淑郎（Syukuro Manabe）和克劳斯·哈塞尔曼（Klaus Hasselmann）为我们所掌握的地球气候知识奠定了基础，并让我们逐步了解人类活动如何影响气候。而乔治·帕里西（Giorgio Parisi）则因在无序与随机现象理论中的突破性贡献而获奖。

所有的复杂系统里，都包含许多各不相同、互相作用的部分。物理学家研究了它们好几个世纪，却很难用数学方法来描述——它们或者由数不清的部分构成，或者受到随机概率的支配。复杂系统也可能是混沌的，比如天气系统，初始值的小小偏差会对之后的状况带来巨大影响。今年的3位物理学奖获奖者，都为人类认知这样的系统及其长期变化作出了贡献。

我们这颗星球的气候，就是众多复杂系统中的代表。真锅和哈塞尔曼因为在开发气候模型上的前沿工作而获得物理学奖。帕里西获奖则是因为对复杂系统理论中的大量问题提出理论解决方法。

真锅淑郞的研究向我们展示了大气中二氧化碳浓度的增加如何提高地面温度。在20世纪60年代，真锅领导开创了地球气候的物理模型。此外，他还是探究辐射平衡与气团垂直输运关系的第一人。他的成果奠定了开发气候模型的基础。

近10年后，克劳斯·哈塞尔曼创造了一个结合了短期天气与长期气候的模型，如此一来，便回答了“为什么天气变化多端、混沌无序，但气候模型仍然可靠”的问题。同时，他还开创了方法用于识别特定的指标和指纹——这些都是自然现象或人类活动在气候中留下的印记。人们用他提出的方法证明，大气温度的升高正是人类排放的二氧化碳所致。

1980年前后，乔治·帕里西发现了无序复杂材料中的隐藏规律。对于复杂系统理论来说，帕里西的发现是最重要的贡献之一。他的发现使理解和描述许多不同而无序的复杂材料和现象成为可能。不仅在物理学界如此，在其他很多看似不相关的领域，比如材料科学、生物学、神经科学、和机器学习领域亦是如此。

温室效应对生命至关重要

200年前，法国物理学家约瑟夫·傅立叶（Joseph Fourier）研究了太阳对地面辐射和地面向外辐射之间的平衡。他认识到了大气在这种平衡中的作用；在地球表面，射入的太阳辐射被转化为射出的辐射，被称为“暗热” (dark heat)。大气吸收这种辐射，并被加热。大气的这种保护作用，也就是当下所谓的“温室效应”。之所以称为温室效应，是因为大气与温室的玻璃相似，允许太阳的热辐射进入，但是会将热量留在其中。然而，大气中的辐射过程要复杂得多。

现在的课题和傅立叶当时所作的研究是一样的——研究地球受到的短波太阳辐射和地球射出的长波红外辐射之间的平衡。在之后的两个世纪里，许多气候科学家在这个研究课题上添砖加瓦。当代的气候模型已经成为了非常强大的工具，不仅能够帮助我们了解气候，还可以了解人类所造成的全球升温。

这些模型由物理定律作为基础，是从用来预测天气的模型发展而来的。天气是用气象量来描述的，比如温度、降水、风或云，并被海洋和陆地上发生的事情所影响。气候模型则是基于天气的计算统计值，如平均值、标准差、最高和最低测量值等。它们不能告诉我们明年12月10日斯德哥尔摩的天气会是什么样，但我们可以用它们来预测当地12月的平均气温和降雨量。

确立二氧化碳的作用

温室效应对地球上的生命至关重要。它控制着温度，因为大气中的温室气体（二氧化碳、甲烷、水蒸气和其他气体）首先吸收地球的红外线辐射，然后释放吸收的能量，加热周围的空气和地面。

温室气体实际上只占据地球干燥大气中的一小部分。大气主要由氮气和氧气构成，这两种气体占据了大约99%的体积，而二氧化碳的体积只有0.04%。最强大的温室气体是水蒸气，但我们无法控制大气中水蒸气的浓度，却可以控制二氧化碳的浓度。

大气中的水蒸气含量高度依赖于温度，由此形成了一种反馈机制。大气中的二氧化碳越多，温度就越高，空气中便会含有更多的水蒸气，从而加剧温室效应并使温度进一步升高。如果二氧化碳水平下降，一些水蒸气会凝结，温度则会下降。

关于二氧化碳影响研究的第一块重要拼图，来自瑞典研究人员和诺贝尔奖获得者斯万特·阿伦尼乌斯（Svante Arrhenius）。值得一提的是，在 1901 年，他的同事、气象学家尼尔斯·埃科赫姆（Nils Ekholm）第一个使用“温室”一词来描述大气的热量储存和再辐射。

到了19 世纪末，阿伦尼乌斯理解了造成温室效应的物理学机制——射出辐射正比于辐射体绝对温度 (T) 的四次方 (T⁴)。辐射源越热，射线的波长越短。太阳的表面温度为 6,000°C，主要发射可见光波段的辐射。地球表面温度仅为 15°C，会重新辐射我们看不见的红外辐射。如果大气不吸收这种辐射，地表温度几乎不会超过 –18°C。

事实上，阿伦尼乌斯当时想要找出导致不久前发现的冰河时代现象的原因。他得出的结论是，如果大气中的二氧化碳水平减半，足以让地球进入一个新的冰河时代。反之亦然——二氧化碳量增加一倍会使温度升高 5-6°C，这个结果在某种程度上与目前的估计非常接近。

二氧化碳效应的先驱模型

20世纪50年代，日本大气物理学家真锅淑郎（Syukuro Manabe）是东京一位年轻有才华的研究人员，他离开了饱受战争摧残的日本，来到美国继续职业生涯。真锅淑郎的研究，就像70年前阿累尼乌斯的研究一样，目的是了解二氧化碳含量的增加如何导致温度升高。然而，相比于阿伦尼乌斯专注于辐射平衡，真锅淑郎在20世纪60年代领导开发了物理模型，将对流引起的气团垂直输送和水蒸气的潜热也结合了进来。

为了将计算量控制在可接受的范围内，他选择将模型降至一维——描述一个40千米公里高、伸入大气的垂直长柱。尽管如此，通过改变假设的大气气体成分测试这一模型仍花费了数百个小时的昂贵计算时间。氧气和氮气对地表温度的影响可以忽略不计，二氧化碳则展现出清晰的效应。大气中的二氧化碳浓度翻倍时，全球气温会上升超过2°C。

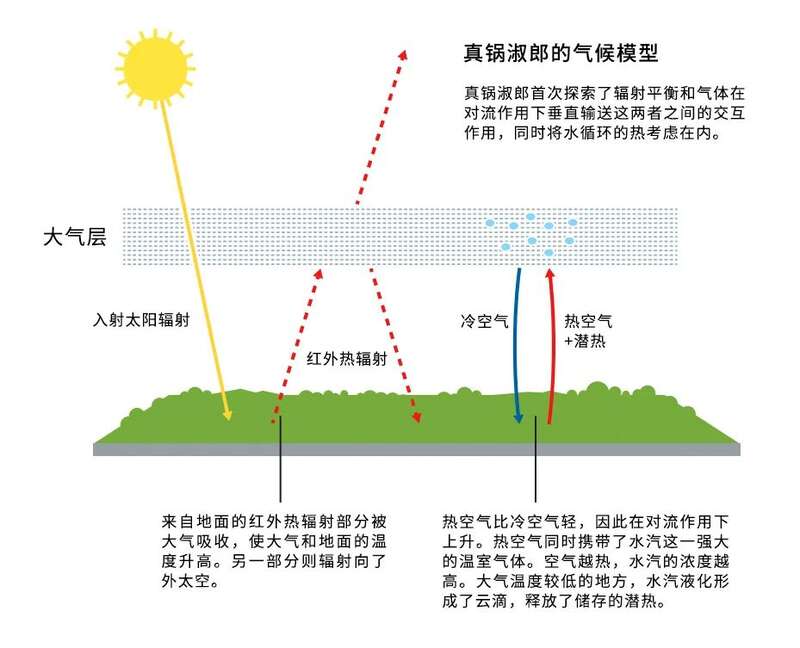
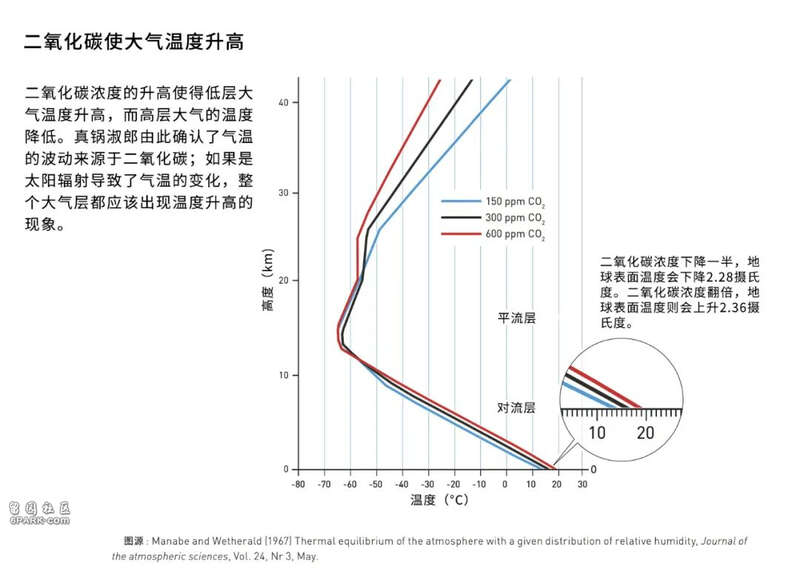
该模型的预测显示升温只在接近地表的地方发生，而上层大气会变得更冷。因此它确认了这种升温确实由二氧化碳浓度上升引起。如果温度变化由太阳辐射变化引起，整个大气应该同时升温才对。

60年前的计算机速度只有如今的几十万分之一，所以这一模型相对简单，但是真锅正确地抓住了关键特征。“你总是要进行简化的，”他如是说，“你不可能与大自然的复杂性竞争，每一个雨滴中都有太多的物理因素了，多到永远不可能去详细地计算每一件事。”在一维模型提供的洞见启发下，真锅在1975年发表了一个三维气象模型。这个模型成为了理解气候秘密的道路上的另一座里程碑。

混沌的天气

大约10年后，真锅和克劳斯·哈塞尔曼（Klaus Hasselmann）用他们的聪明才智找到了一条道路，将快速、混沌、难以计算的天气变化与气候联系在了一起。由于太阳辐射在地理和时间层面的分布十分不均，我们的星球天气变化剧烈。地球是球形的，所以与接近赤道的低纬度地区相比，高纬度地区接收到的阳光少得多。此外，地球的自转轴是倾斜的，造成了太阳辐射量的季节性变化。冷热空气的密度差异造成了不同纬度、海陆之间、以及高低气团间巨量的热交换，它们驱动着地球上的天气活动。

众所周知，准确预测超过10天后的天气充满挑战。200年前，著名的法国科学家皮埃尔-西蒙·拉普拉斯（Pierre-Simon de Laplace）宣称，如果能知道宇宙中所有粒子的位置和速度，我们应该可以算出过去和未来发生在这世界上的所有事情。原则上，这应该是对的。牛顿在3个世纪前提出的运动定律也能够描述大气中空气的运动。而它们是确定性的，其中不存在偶然。

然而，在说到天气时，没什么比这错得更离谱了。一部分原因是，现实中不可能做到足够精确，来确定大气层中每个点的气温、压力、湿度或风况。此外，这些方程是非线性的；初始值的微小偏差将使一个天气系统以完全不同的方式演变。蝴蝶在巴西拍打翅膀是否会导致得克萨斯州刮一场龙卷风——基于这一问题，该现象被命名为蝴蝶效应。在现实中，这意味着长期天气预报是不可能做到的 —— 天气是混乱的。这一发现由美国气象学家爱德华·洛伦茨在20世纪60年代提出的，他为今天的混沌理论奠定了基础。

给噪声数据赋予意义

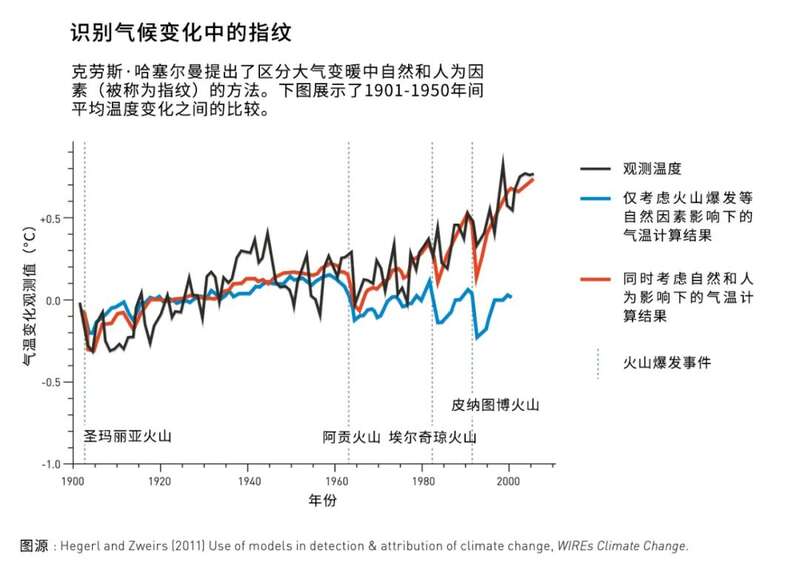
既然天气是一个混沌系统的典型例子，我们又怎么能给未来几十年或几百年建立一个可靠的气候模型呢？1980年前后，克劳斯·哈塞尔曼证明，混沌变化的天气现象能够被描述为快速变化的噪声，从而将长期气候预测建立在一个坚实的科学基础上。此外，他还提出了方法，用以识别人类对所测得的全球温度的影响。

20世纪50年代，作为德国汉堡的一名年轻物理学博士生，哈塞尔曼从事燃料动力学研究，然后开始建立对海浪和洋流的观察和理论模型。他搬到了美国加利福尼亚，继续从事海洋学研究，遇到了查尔斯·戴维·基林等同事。基林于1958年在夏威夷的莫纳罗亚天文台启动了大气二氧化碳测量项目，如今已经成为持续时间最长的大气二氧化碳测量项目——基林也因此成为传奇。那个时候哈塞尔曼还不知道，在他后来的工作中将经常使用基林曲线，这个曲线显示了二氧化碳水平的变化。

如何从杂乱的天气数据中得到一个气候模型，可以用遛狗来打个比方：狗子窜前跑后左蹦右跳，还会绕着你的腿转圈圈。如何利用狗的足迹来弄清你是在走路还是站着？或者你是在慢步还是小跑？狗的足迹就像是天气，而你的路线则是计算出来的气候。使用混乱的、如同噪声的天气数据，有可能对气候的长期趋势得出结论吗？

一个额外的困难是，影响气候的因素随时间的波动也是千差万别的——有些变化迅速，比如风力或者气温，有些则十分缓慢，比如冰盖融化和海洋变暖。举例来说，整体升温1°C，对海洋来说可能需要1000年，但对大气来说只需要几个星期。关键技巧是将天气的快速变化作为噪声纳入计算，并显示这种噪声如何影响气候。

哈塞尔曼建立了一个随机的气候模型，这意味着偶然性是内置于这个模型中的。他的灵感来源于爱因斯坦的布朗运动理论，也叫随机游走。利用这一理论，哈塞尔曼证明了快速变化的大气层可以引起海洋的缓慢变化。

辨别人类影响的痕迹

气候变化的模型完成后，哈塞尔曼提出了方法，用来识别人类对气候系统的影响。结合观测和理论考量，他发现他的模型充分包含了有关噪声和信号属性的信息。举例来说，太阳辐射、火山颗粒物或温室气体水平的变化会留下独特的信号，即指纹，是可以被分离出来的。这种识别指纹的方法也可以应用于人类对气候系统的影响。哈塞尔曼因此为进一步研究气候变化扫清了道路，这些研究利用大量的独立观测数据，证实了人类影响气候的痕迹。

通过卫星测量和天气观测等手段，气候的复杂相互作用过程被更彻底地描绘出来，气候模型也因此越发完善。模型清楚地表明，温室效应正在加速；自19世纪中期以来，大气中的二氧化碳水平已增加40%。地球的大气层已有几十万年没有这么多的二氧化碳了。相应地，温度测量显示，在过去的150年里，世界已升温1 °C。

真锅淑郎和克劳斯·哈塞尔曼本着诺贝尔的精神，为我们对地球气候的认知打下坚实的物理基础，为全人类做出极大贡献。我们再也不能说我们不知道了——气候模型是明确无误的。地球在升温吗？是的。是因为大气中的温室气体的增加吗？是的。这能完全用自然因素来解释吗？不能。人类的排放是升温的原因吗？是的。

无序系统的方法

1980年前后，乔治·帕里西展示了他的发现：表面随机的现象是如何被隐藏的规则所控制。他的工作现在被认为是对复杂系统理论的最重要贡献之一。

复杂系统的现代研究植根于统计力学，由麦克斯韦（James C. Maxwell）、玻尔兹曼（Ludwig Boltzmann） 和吉布斯（J. Willard Gibbs）在19 世纪下半叶创立。统计力学这个领域，就是由吉布斯在1884年命名的。统计力学脱胎于一种观念，即需要一种全新的方法来描述由大量粒子组成的系统（例如气体或液体）。这种方法必须将粒子的随机运动考虑在内。也就是说，这种方法的基本思想是计算粒子的平均效应，而不是单独研究每个粒子。举例来说，气体中的温度是气体粒子平均动能的标志。因其能够为气体和液体的宏观特性（如温度和压力）提供微观解释，统计力学取得了巨大的成功。

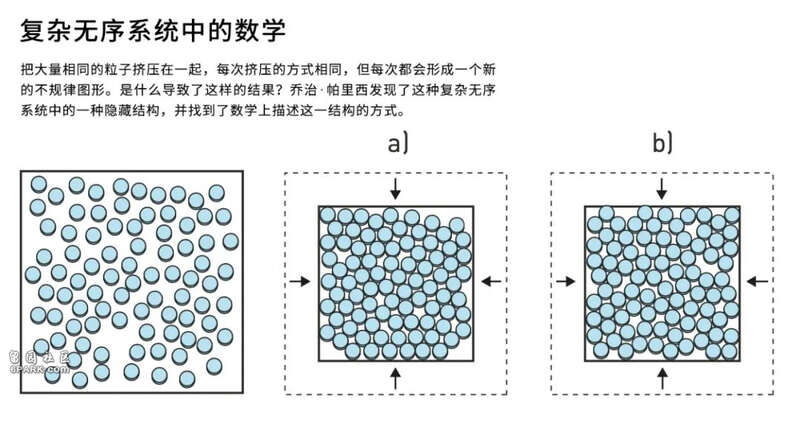
我们可以把气体中的粒子看作是飞来飞去的小球，飞行的速度随着温度的升高而增加。当温度下降或压力增加时，小球首先凝结成液体，然后变成固体。这种固体通常是晶体，其中的小球按规则排列。但是，如果这种变化发生得很快，小球可能会构成不规则的形状，即使液体进一步被冷却或挤压，形状也不会改变。如果重复该实验，即使变化以完全相同的方式发生，小球也将呈现出一种全新的形状。结果为什么会不一样呢？

认识复杂性

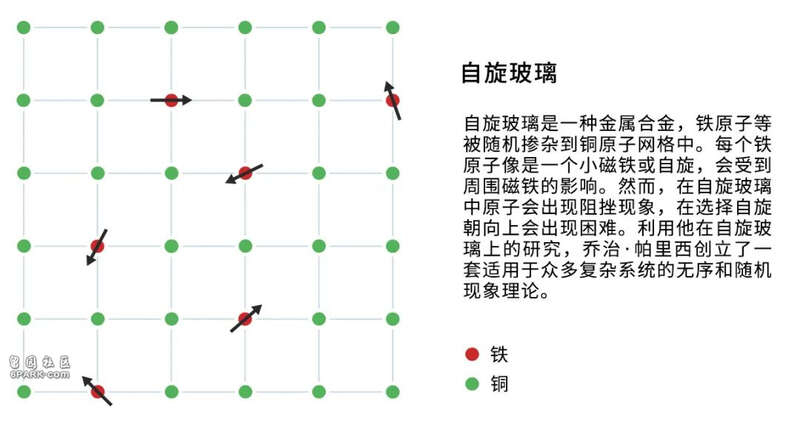
对于普通玻璃和沙砾之类的颗粒材料来说，这些受到挤压的小球是一个简单模型。然而，帕里西最初研究的却是一种不同的系统——自旋玻璃（spin glass）。这是一种特殊类型的金属合金，例如，铁原子随机混入铜原子的网格。尽管网格中只有几个铁原子，它们却以一种激烈但不可名状的方式改变了材料的磁性。每个铁原子就像一个小磁铁，它的自旋受到附近其他铁原子的影响。在普通磁铁中，所有自旋都指向同一个方向，但在自旋玻璃中，自旋是受到阻挫的：一些原子对的自旋想要指向同一个方向，另一些却想指向相反方式——如此一来，它们如何找到最佳的指向呢？

在介绍自旋玻璃的书中，帕里西写道，研究自旋玻璃就像欣赏莎士比亚创作的人间悲剧。如果想同时和两个人成为朋友，而他们却是死敌，你就会受到阻挫。在古典悲剧中更是如此，情绪高涨的朋友和仇敌在舞台上狭路相逢，怎样尽可能降低台上的紧张气氛呢？

自旋玻璃及其奇妙的特性为复杂系统提供了一个模型。20世纪70年代，包括几位诺贝尔奖获得者在内的许多物理学家都在寻找方法，来描述这种神秘而又阻挫的自旋玻璃。他们使用的方法之一就是“副本方法”（replica trick）。这是一种数学技巧，能够同时处理一个系统的许多副本。然而，这个方法最初被应用在这个物理问题时，却是行不通的。

1979 年，帕里西展示了如何巧妙地使用副本方法来解决自旋玻璃问题，取得了决定性的突破。他在副本中发现了一个隐藏结构，并找到了一种描述它的数学方法。很多年后，帕里西的解决方案才在数学上被证明是正确的。此后，他的方法被用于研究许多无序系统，并成为复杂系统理论的基石。

阻挫的果实多种多样

自旋玻璃和颗粒材料都是阻挫系统的例子。在这种系统中，不同的成分必须以一种在反作用力之间折衷的方式排列。需要解决的问题是，它们如何行事，又会产生怎样的结果。帕里西是回答许多不同材料和现象中此类问题的大师。他对自旋玻璃结构的根本性发现影响深远，不仅影响了物理学，还影响了数学、生物学、神经科学和机器学习等领域，因为所有这些领域中都有与阻挫直接相关的问题。

帕里西还研究了许多其他现象，在那些现象中，随机过程在结构的形成和发展过程中起着决定性作用。帕里西还解决了以下问题：为什么冰河时代会周期性地重复出现？是否有一种更为通用的数学方式来描述混沌和湍流系统？还有，成千上万只椋鸟成群结队飞行时呈现的图案是如何形成的？这个问题似乎与自旋玻璃相去甚远。

然而，帕里西表示，他的大部分研究都涉及简单行为如何导致复杂的集体行为，这既适用于自旋玻璃，也适用于椋鸟。