
请听题:
如何将苹果平均一分为二,还能保证它长时间的新鲜?
这是一个严肃的科学问题,已经困扰了人类数学家25年之久。
根据常识,就是要保证果肉暴露在外面的面积最小,也就是切片的面积最小。如果跨越到更高的维度,是否依然成立?
这就是1995年,由三位数学家提出的一个几何学猜想。

现在,这个难题被一位华人统计学博士,解决了。
成果一经发布,就迅速引起了数学、理论计算机科学、统计学等多个领域的科学家的关注。
他们一致认为,数学大师、菲尔兹奖得主,原本猜想的提出者Jean Bourgain(让·布尔甘)一定会对这一进展感到兴奋。
毕竟,在他去世前(2018年)的几个月里还在关心这一问题进展,但终其一生都未能解决。

困扰数学家25年的几何问题1984年,著名数学家让·布尔甘提出了一个猜想。
一个任意维度的凸体,用低一维的平面去平分,那么存在一个常数c,让凸体至少存在一个切面的面积大于c。
换句话说,如果你一刀平分“任意维度空间的西瓜”,随便你怎么劈,总有一个切面总大于c。
(Ps:以往的科学家用的是苹果的例子。但准确来说不能选苹果,因为苹果上下是凹的。)
在3维空间中,这个结论似乎很好理解,因为无论西瓜长成什么奇形怪状,总不可能在每个角度都细长。
像下面这样的长西瓜,竖直切下去,切面很小,可以你也可以水平切开平分它,这样切面就会很大。

但在3维世界中正确的事情,到了高维空间却不一定成立。
这个问题后来被布尔甘自己证明,但数学家们并不满足于用平面切西瓜,而是希望能找到一个更小的切面,它可以是曲面。
而这恰好是1995年Kannan、Lovász和Simonovits三人提出的KLS猜想关心的问题:用来平分的最小曲面面积是多少?
以二维空间里的一个三角形为例。
这个最小的“曲面”是一段圆弧。用圆弧来平分一个三角形,中间的线长度最短,而最佳“平面”——直线——的效果略差。
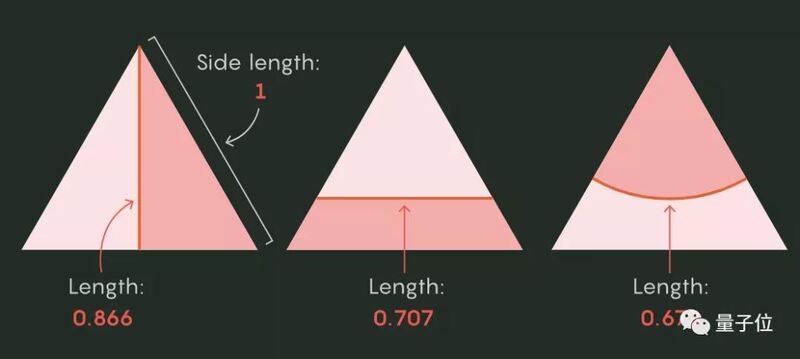
△ 如何用最小“切面”平分三角形(来源:Quanta Magazine)到了更高维度的空间中,二等分的最佳平面和最佳曲面差距会变大吗?切面的面积是否和维度d有关?
这个问题已经不再是纯粹的数学问题。
普林斯顿大学数学系教授Assaf Naor表示,KLS猜想在纯粹的数学和理论计算机科学中都很重要。
KLS猜想的结果,直接关系到随机行走算法的运行时间,如机器学习模型中采样问题。
所以最后解决这个几何问题的学者,都并非几何学的专家,而是来自计算机界。
用统计方法解决他经过数学家的抽象,KLS猜想就像一个封装着气体的容器,找到最佳切面就是寻找容器的“瓶颈”。
想象一个哑铃形状的容器,里面有一个气体分子在随机运动,哑铃中间连接部分越细,分子就越难跑到另一侧。
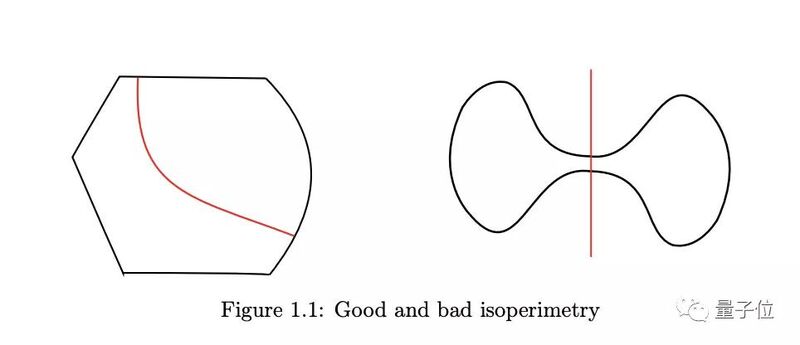
△哑铃形的平分切面很小(来源:Yin Tat Lee论文)现在人们想知道,在高维空间,这个凸的容器最细的地方有多细。(当然,哑铃并非是凸的。)
2012年,Eldan通过引入一种称为随机定位的技术,来降低这个问题与维度上界。(到底是维度d的几次幂。)
2015年末,华盛顿大学的Vempala和Yin Tat Lee改进了Eldan的随机定位,以进一步将KLS因子(用于描述瓶颈是否存在)降低到维度的四次根d1/4。
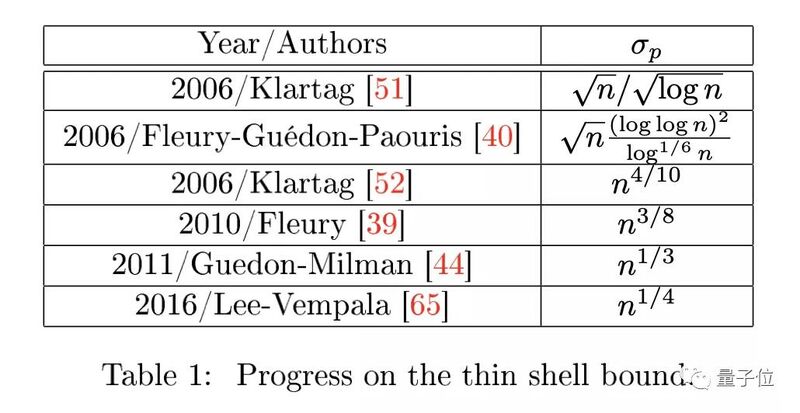
△ KLS猜想的上界不断降低(来源:同上)甚至,他们还将幂指数降低到几乎为0,由于d的0次幂总是等于1,Lee和Vempala似乎证明了KLS因子是一个与维度无关的常数。
他们在arXiv上发布了他们的论文。但是几天后,这篇文章就被人发现了一个缺陷,他们关于d0的证明是错的。
之后,二人修改了文章,把界限重新调整到d1/4。几年来,研究人员认为KLS猜想的探索已经到此终结了。

不过他们还在论文中,保留了d0证明的一些想法。这也为后来的突破埋下伏笔。
他们的论文引起了另一位统计学者Yuansi Chen的注意。
Chen当时是加州大学伯克利分校的统计学研究生,他正在研究随机采样方法的混合率。而随机抽样是许多类型统计推断中的关键,例如贝叶斯统计。
Chen深入研究文学,花了数周时间试图填补Lee和Vempala的证明中的空白,但依然没有解决。
于是他转变了思路,在Lee和Vempala的思想指导下,他找到了一种方法,采用递归来降低KLS因子上界。
经过反复迭代,这种方法将KLS猜想问题再次拉回到d0的上界。
这一结果意味着,高维凸形物体不会有哑铃那样的结构。
该定理的结果意味着,在n维凸体中随机行走,遍历整个图形的速度比我们之前预想得要快得多。
这将有助于计算机科学家对不同的随机采样算法进行优先级排序。
三个计算机相关的科学家虽然表面看上去,这三位学者似乎跟数学没什么关系。
但仔细翻看他们的履历,他们都曾跟数学结下了不小的缘分。
首先,直接与研究相关的这位统计学博士后——Yuansi Chen (陈远思,音译)。

今年年初,他开始在杜克大学统计科学系担任助理教授的职位。

主要研究方向是统计机器学习、优化以及在神经科学中的应用,尤其对其中域适应性、稳定性、MCMC采样算法、卷积神经网络和计算神经科学中出现的统计问题感兴趣。
2019年,他在加州大学伯克利分校统计系获得博士学位。
其博士生导师是著名华裔统计学家、UC伯克利统计系和电子工程与计算机科学系终身教授郁彬。

在攻读博士之前,他还在法国Ecole Polytechnique获得了应用数学专业的工程师文凭。
随后,前往在苏黎世联邦理工学院ETH Foundations of Data Science(ETH-FDS)做博士后研究。
而启发Yuansi Chen数学灵感的,是两位计算机科学家。
Yin Tat Lee (李贤达,音译)和Santosh S. Vempala。

李贤达,目前是华盛顿大学助理教授,本科毕业于香港中文大学。
2012年从港中文大学毕业后,前往麻省理工学院攻读博士学位,随后前往微软研究院做博士后研究。
他的研究方向主要在算法方面,包括凸优化、凸几何、谱图理论和在线算法等广泛的课题。
以往的研究里,他曾结合连续数学和离散数学的思想,大幅提升了在计算机科学和优化中许多基本问题的算法,比如线性编程和最大流量问题。

他曾获得SODA最佳论文奖、NeurIPS 2018最佳论文奖、NSF职业奖。
去年他还获得了有“诺奖风向标”之称的斯隆奖,以及美国最大的非政府奖学金之一——帕卡德奖学金。
再来看Santosh S. Vempala,佐治亚理工学院计算机科学教授。
主要研究领域是理论计算机科学,还抽样、学习、优化和数据分析的算法工具;随机线性代数,高维几何。
他曾在卡内基梅隆大学攻读博士学位,本科毕业于印度理工学院的计算机专业,曾获NSF职业奖、斯隆奖等奖项。
在来到佐治亚理工学院之前,他曾担任MIT应用数学系担任教授、UC伯克利米勒研究员。
数学家:不可思议随着陈远思论文一发布,迅速就引起了数学界的学者关注。
不光是因为此前的错误证明,还由于陈远思这个名字在数学界十分陌生,研究人员对待这一成果十分谨慎。
但他的方法很容易被验证。
早期研究过KLS猜想的以色列数学家BoázKlartag,就在第一时间看了论文。
我基本上立即停止了我正在做的一切事情,并检查了这篇论文。
这篇论文是100%正确的,这一点毫无疑问。

除了一众数学家关注之外,还引起了理论数学家、统计学等领域的注意。
哈佛大学计算机科学教授、微软研究院前新英格兰首席研究员Boaz Barak则发推祝贺。
并表示这是一个非常重要的突破,加速了对近似凸体体积的研究。

但点赞祝贺之余,也有不少学者表示十分遗憾。
因为提出这一猜想的人菲尔兹奖得主布尔甘已于2018年去世,如果他还在的话,一定会为这一进展感到兴奋。
据QuantaMagazine报道,布尔甘曾在去世前几个月,联系了他的朋友、特拉维夫大学教授Vitali Milman,询问这一猜想是否有任何进展,想在离开之前知道答案。
但Vitali Milman说,布尔甘在这一问题上,花费的时间和投入的精力比任何其他问题多得多。没想到,最后这个问题却被统计学解决了。


