猩猩、鹦鹉、蜜蜂,甚至连老鼠都会数数,它们甚至还会计算?没错,这种能力是动物们物竞天择的优势,它们的数学天赋已经被科学家研究过很多次了,每次结果都很有趣。
前奥数冠军霍格尔·丹贝克的这本新书,通过许多类似的趣事,帮作者重拾数学的乐趣,治好数学恐惧症——他也是我们此前推荐的《三个逻辑学家去酒吧》作者。
《你学的数学可能是假的》▼▼▼
据说,数学把人分成两种,一种甘之如饴,一种对它怕得要命。其实,数量与几何,始终深深根植于每个人的意识当中,只是人们往往忽略了这一点。几个月大的婴儿就已经会简单的加法计算,就连小动物都会计算,当它们计算时,也会跟我们犯一样的错误。
从天生的数量感,到超简单的计算技巧,再到优雅的证明过程,霍格尔·丹贝克为我们展现了老师没教过已经还给老师的美丽数学世界。
狮子如何识别敌人数量?
尽可能准确地掌握对手的数量,这对动物很重要。谁若是低估了敌方数量,有时就会付出生命的代价。因为计数中的一个小小错误,可能会带来致命的后果。
那么,动物是如何获知同类的数量的呢?1994年,剑桥大学的动物学家在坦桑尼亚对狮子进行了一项有趣的研究。大自然中常常有多达20头的母狮子群居,狮群之间通常井水不犯河水,都有自己的领地。然而,狮群之间总是不期而遇,甚至会有激烈的战斗。
多数时候数量较多的狮群会获胜。吼声在狮子的交流中起着重要的作用。狮子会单独吼叫,也会成群吼叫,它们一头接一头地轮流发出狮吼,类似合唱团唱歌。研究者们录下了1头狮子的吼声和由3头狮子组成的小群体的吼声。之后,他们通过扬声器将录下的吼声播放给200米外的母狮群听。母狮们就会不断地听到陌生的狮子的吼声。
扬声器的小伎俩开始起作用了:这些大型猫科动物听得非常认真,然后根据自己狮群的大小来决定是否接近这些「入侵者」。如果扬声器发出1头狮子的吼声,那么由3头或更多母狮组成的狮群,每10次中有7次会进攻,也就是攻击概率为70%。但如果咆哮声是由3头狮子发出来的,这些母狮子就明显更加谨慎了。它们自己的狮群要达到5头以上,才会冒着70%的风险发动攻击。
扬声器实验表明:狮子会通过吼声来识别出有多少敌人。它们敢不敢攻击入侵者,取决于对手的狮群大不大。它们会比较双方参与战斗的狮子数量,只有当己方占优势时,才会发起进攻。
谁是动物王国的数学天才?
答案是人类最亲近的灵长类「亲戚」——黑猩猩。

1981年,《自然》杂志上发表的一篇论文引起了轰动。两位研究员报告说,黑猩猩不仅能知晓数量,甚至还能做分数计算。在黑猩猩面前有一个装有有色液体的半满玻璃杯,它必须在半个苹果和3/4个苹果中进行选择,与相应的杯子匹配。黑猩猩的抽象能力竟然足以使其辨识出:半满的玻璃杯与半个苹果是匹配的。研究者们还证明,黑猩猩能在头脑中将1/4和1/2合并成3/4,它们甚至能进行基本的分数加法计算。
除此之外,黑猩猩的实验也表明:灵长类计算数字的原则,与我们人类完全相同。1987年,学者们进行了「巧克力的诱惑」实验,他们在黑猩猩面前放了两个抽屉,每个抽屉里都放了几块巧克力。研究人员假设,这些动物会主动伸手抓向装有最多块巧克力的抽屉。一旦它们决定了一个抽屉,另一个抽屉就会被迅速撤回,它们就无法拿到被撤回的抽屉里的巧克力了。
研究人员想在实验中发现灵长类加法水平究竟如何,他们就在抽屉里将巧克力分为两小堆:在一个抽屉中,将4块巧克力堆在一起,还有一块巧克力是单独放的;在另一个抽屉中放了两堆巧克力,各有3块——而黑猩猩通常会选择放着最多巧克力的抽屉,太优秀了。
会抢答的鹦鹉
众所周知,鹦鹉能完美地模仿声音和音调,但这只名叫亚历克斯的灰鹦鹉,并不是简单重复它从主人那儿听到的东西,它是真的能明白这些问题的意思。

这只鹦鹉在2007年去世之前,学会了识别超过100个物体,7种颜色和5种形状。它还可以简单分辨大小、材料、形状、颜色和数字。当主人佩珀伯格向它展示1块木头和1个羊毛线团,并问它这是什么材料,亚历克斯会回答「羊毛」或「纸」。亚历克斯的计算能力也让人印象深刻。例如,主人向亚历克斯伸出两把钥匙,问道:「有多少把?」亚历克斯很快回答:「两把。」
它的计算能力还不止如此。主人向它展示了一个托盘,托盘上有2个绿色、5个蓝色的立方体,还有几辆绿色和蓝色的玩具车。然后,她问道:「有多少个绿色方块?」虽然亚历克斯是第一次看到以这种组合放置的物品,但它依然给出了正确答案:「2。」
亚历克斯甚至能做简单的加法。在实验中,亚历克斯面前有两个倒扣的不透明塑料杯,下面藏着坚果或糖。只有当实验者抬起其中一个杯子时,亚历克斯才能看到它下面有多少坚果。之后,实验者再抬起第二个杯子。亚历克斯每次有10—15秒来得知每个杯子下的物体数量。接着,实验者试着与鹦鹉进行目光接触,并问道:「总共有多少坚果?」这时,鹦鹉已经看不见杯子下面的坚果了。在总计48次单独实验中,鹦鹉一共只犯了7次错误。有视频有真相,一起看看鹦鹉是怎么答题的:
柯基犬也会函数求导?
照片里这只天赋惊人的狗叫埃尔维斯,是一只威尔士柯基犬,它的主人蒂姆·彭宁斯是一位数学老师。

彭宁斯会定期和埃尔维斯一起出去溜达,在宽广的湖边惬意地散步,与此同时,他总是会带上狗狗最爱的玩具:一个网球。
(图片为示意图,来源自网络)
彭宁斯通常沿着水位线在沙滩上散步,把球斜着扔进水里。此时,这位数学老师发现,埃尔维斯从来没有过直接游向它最喜欢的球,而是在沙滩上跑了几米之后才一个急转弯,跳进水里游完最后几米。
数学家的直觉,让彭宁斯开始思考为什么埃尔维斯没有走直线。很快,一切真相大白:狗狗会在沙滩上跑一段距离,因为它奔跑比游泳快得多,这样它就能花比直线游泳更少的时间去拿到球。
(图片为示意图,来源自网络)
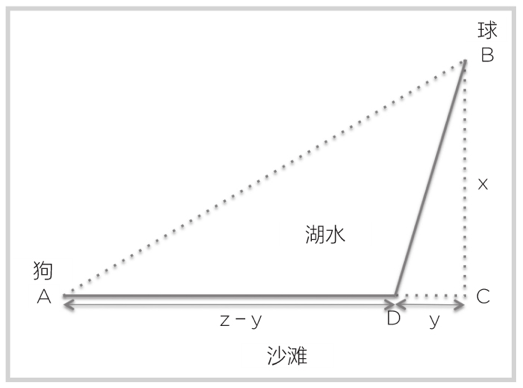
彭宁斯分析了这个问题,并指出:要找出最快的路径,你必须掌握微分学,因为求相同时间下最短的路径就等于求一个函数的最小值,而没有人可以立马说出这个最小值。埃尔维斯站在A点,网球在水里漂向了B点。
为了计算出埃尔维斯要用多少时间才能拿到球,我们必须知道它走过的路程、奔跑的速度和游泳的速度。它在沙滩上从起点A点跑到D点,这条路线的距离是z-y。然后,它从D点游到B点,根据勾股定理,这段距离的长度是根号下x平方+y平方。我们把奔跑速度设为g,游泳速度设为s。根据时间=距离/速度,就得到了计算总时间的公式:
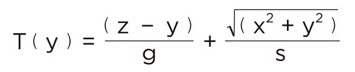
我们要求这个函数的最小值,就要求它的一阶导数:
函数的最小值为T'(y)=0。最后,我们就得到了答案:
彭宁斯已经指出,埃尔维斯以6.4米/秒的速度奔跑,并以0.9米/秒的速度游泳。由此得出y=0.14x。
这就是说,狗狗在沙滩上跑了很长一段时间,突然转向,最后游完剩下的路程。在彭宁斯所做的35次试验里,埃尔维斯几乎每次都会选择非常接近最优解的路线。但是,这就等于埃尔维斯真能区分出或计算出函数曲线上升或下降的趋势吗?这就有点儿让人难以置信了。有可能,埃尔维斯只是对如何以最快速度拿到心爱的网球有一种良好的直觉。它经常在沙滩上嬉戏,在水里游泳,它就在这当中获得了经验。但也许,这也是某种来自演化与遗传的数学直觉,可以帮动物们更有效率地移动。

















